Как объяснить ребёнку проценты на простых жизненных примерах?
Как объяснить ребёнку проценты на простых жизненных примерах?

СОДЕРЖАНИЕ
С понятием процентов мы сталкиваемся практически ежедневно (в банковской сфере, при подсчёте ингредиентов для приготовления блюд, чтении состава продуктов на упаковке и др.), поэтому знание данной темы будет помогать ребёнку в жизни, даже если он не свяжет свою жизнь с математикой. Но далеко не каждый ученик понимает, как работать с процентами с первого объяснения учителя в школе — некоторым необходимы более подробные разъяснения.
Мы расскажем вам, что такое проценты, об их связи с дробями, как производить математические операции с процентами, и что делать родителям, чтобы ребёнок понял тему процентов по-настоящему, и научился решать задачи на проценты.

Понятие процента: как рассказать о нём школьнику простыми словами?
Слово «процент» происходит от латинского «pro centum», что в переводе означает «на сто». Процент — это одна сотая часть числа, которая в математике применяется для обозначения части чего-нибудь относительно целого. На при письме проценты указывают с помощью значка «%». Например, 15% от целого числа 60 будет 9 (15 частей по 9 каждая).
Чтобы школьник лучше понял, что такое проценты, лучше взять понятный ему наглядный пример вместо абстрактных чисел. Купите в магазине конфеты в виде драже, сядьте с ребёнком за стол и положите в ряд скажем 100 драже — это и будет 100%. 1 драже будет означать 1%, 2 драже — 2%, 3 драже — 3% и. т. д.
Пусть вначале ребёнок откладывает драже-проценты в другой угол стола, чтобы весь процесс происходил у него на глазах. Так, 50 драже — это 50% (половина всех купленных конфет). Пусть ребёнок съест, скажем, 11 маленьких драже. Укажите, что он съел 11% конфет, и, следовательно, осталось 89% от всех конфет которые были в пакете изначально.
Для лучшего понимания дайте ученику задание пересчитать оставшиеся драже. Такие примеры можно повторять, пока школьник не разберётся во взаимосвязи процентов и реального количества конфет, но, постепенно уходя от наглядности.
На следующем этапе уже можно рассказывать о процентах, оперируя воображаемыми конфетами, ягодами или другими объектами, а затем переходить к абстрактным математическим числам.
Где встречаются проценты в повседневной жизни, и почему их важно изучать?
Если тема процентов слишком сложна для понимания, ребёнок может выражать нежелание её осваивать, капризничать, раздражаться. От того, как в этой ситуации поведёт себя взрослый, будет во многом зависеть, насколько быстро ученик преодолеет этот эмоциональный кризис.
Первое, что нужно сделать — выслушать ребёнка, дать ему знать, что его чувства важны и поняты, а затем спокойно рассказать (а лучше даже показать на житейских примерах), какие преимущества даст ему знание процентов и умение выполнять математические операции с ними:
В магазине игрушек (или других товаров, которые интересны ребёнку). Покажите школьнику ценники, где указывается процент скидки на интересующую его покупку, и объясните, что без знания процентов он не сможет посчитать сумму денег, которую нужно заплатить, и оценить, хватит ли средств на совершение покупки.
Например, конструктор стоит условные 1.000 рублей, но на него действует скидка в размере 30%. Какова реальная стоимость конструктора?
Можно попробовать использовать приём вовлечения ребёнка в освоение темы процентов, пообещав купить ему конструктор, когда он сам сможет вычислить его стоимость.
В банке. Если у вас есть банковский вклад или кредит, вы можете взять ученика с собой в банк, рассказать и показать, как понимание, процентной ставки по кредиту, скажем, на автомобиль или смартфон для ребёнка помогает рассчитывать семейный бюджет.
Объясните, что если взять кредит, не ориентируясь в подсчёте процентов, можно отдать все свободные деньги банку, и не останется на развлечения или даже бытовые нужды.
В компьютерной игре. Если ребёнок — увлечённый игрок, то весьма вероятно, что ему приходится сталкиваться в процессе игры с ситуацией, когда у персонажа, за которого он играет, остаётся, например, 20, 35, 68% ресурса (жизни).
Расскажите ребёнку, что если он хочет прогрессировать и повышать свой уровень, необходимо правильно оценивать ресурсы. А без знания процентов делать это проблематично. Высок риск неверно рассчитать силы и в итоге проиграть.

Как проценты связаны с дробями: вычисление процентов в математике
Для того, чтобы ученик усвоил, как проводить математические операции с процентами, необходимо убедиться, что он хорошо понял тему дробных чисел и дробей, которую проходят в школе перед тем как взяться за проценты.
Объяснять, как работать с дробями и процентами, эффективнее всего пошагово, следуя принципу «от простого к сложному»:
Представить его можно в виде обычной дроби как 1/100 или 0, 01 (в виде десятичной дроби): 1% = 1/100 = 0,01. Чтобы записать любое количество процентов в виде дробного числа, необходимо проценты всегда делить на 100. Пусть ребёнок запомнит данное правило. Чтобы он не заучивал его как словесную формулировку, а понял сам принцип, запишите вместе с ним несколько примеров: 15% = 15/100 = 0,15, 87% = 87/100 = 0,87 и. т. д.;
Например: 25% — это четверть целого числа; 50% — половина целого; 75% составляет 2/3 целого; 100% — целое число.
Нарисуйте 4 квадрата, в каждом из которых по 100 клеточек, и пусть ребёнок заштрихует 25 клеточек (25%) в 1-м квадрате, 50 во 2-м, 75 в 3-ем, и все 100 клеточек в 4-м. На первых порах разрешите ему брать такую импровизированную шпаргалку на уроки математики (по согласованию с преподавателем), и использовать её при выполнении домашних заданий. Со временем школьник запомнит основные проценты, и сможет решать задачи и примеры без помощи таблички.
Например: 265% = 265/100 = 2,65. Пусть ребёнок выполнит несколько заданий по аналогии для закрепления результата.
Рассмотрите вместе со школьником обратную ситуацию, когда дробь нужно перевести в проценты. Действовать необходимо по правилу, которое также следует выучить: для перевода дроби в проценты нужно дробь умножить на 100. Например: 0,07 = 0,07х100 = 7%, 4/5 = 4/5х100 = 4х100/5 = 80%.
Когда вы убедитесь что ребёнок понял оба правила, дайте ему серию заданий, где нужно будет переводить то дроби в проценты, то проценты в дроби, чтобы навык решения выработался скорее.
Наглядный способ объяснения процентов на практическом примере
Объяснять принципы вычисления доли от общего числа (100%) можно и приводя наглядные примеры процентов.
Сделать это легко в житейской ситуации, как в уже ранее упомянутом примере с магазином игрушек.
Допустим, ребёнку понравилось в магазине игрушка за 427 руб, на которую действует скидка в размере 30%.
Поясните, что нужно делать, чтобы понять, достаточно ли у нас денег на покупку:
Посчитать, сколько будет 1% от цены игрушки. Полную стоимость игрушки берём за 100% (427 руб в нашем случае равно 100%). Чтобы вычислить 1%, нам необходимо 427/100 = 4, 27 (4 рубля 27 копеек равны 1% от стоимости игрушки (от 427 рублей).
Выяснить размер скидки в рублях (нам известно, что скидка составляет 30%, но мы пока не знаем, сколько это будет в деньгах). Для этого берём 1% от цены игрушки — 4 рубля 27 копеек, и умножаем на 30% (скидку): 4, 27х 30 =128, 1. Значит, 30% от 427 рублей — это 128 рублей 10 копеек.Так мы получаем нашу скидку в денежном эквиваленте.
Понять, сколько будет стоить игрушка с учётом скидки.
Мы знаем:
Значит, нам необходимо из полной стоимости игрушки (427 рублей) вычесть сумму скидки (128 рублей 10 копеек), и мы получим актуальную цену: 427-128,1 = 298,9 (298 рублей 90 копеек).
Итак, получается, что игрушка стоит 298 рублей 90 копеек.
После проведения подсчётов, если ребёнок старательно вникал в объяснение, задавал вопросы, отправляйтесь вместе в магазин и приобретите для него игрушку. Это, конечно, не обязательная опция, но желательная рекомендация, которая имеет как практический, так и воспитательный эффект, который заключается в том что:
ребёнок, который хочет получить игрушку своей мечты, с большим желанием будет вникать подсчёты процентов, даже если тема даётся ему с трудом, ведь он понимает, что от его вовлечённости зависит, купят ему игрушку или нет (личная заинтересованность = мотивация);
искреннее желание понять, как работать с процентами, способствует скорейшему усвоению темы;
ученик поймёт, что знание процентов необходимо не только чтобы решать скучные примеры и задачи в школе, но и чтобы совершать покупки, подсчитывать бюджет, и не тратить больше денег чем необходимо.
Три типа задач на проценты для школьников
Существует 3 разновидности математических задачек на проценты для школьников, которые нужно научиться решать:
Вычисление числа по заданному количеству процентов, которое оно составляет.
Нахождение процентов от числа.
Определение, сколько процентов одно число составляет от другого.
Приведём примеры каждого вида задач с алгоритмом их решения:
Задача №1
Папа решил купить Роберту удочку для рыбалки. Сегодня в магазине рыболовных принадлежностей скидка на все товары 40%. Помоги папе найти модель удочки для Роберта, если без скидки она стоит 7200 рублей.
Решение:По условию задачи нам известны: цена удочки без скидки (7200 рублей) и размер скидки в процентах (40%); Мы имеем в виду,что 40% — это скидка от полной стоимости удочки.
Значит, цена 7200 рублей — это 100% стоимости удочки.
Нам для решения задачи нужно выяснить, сколько рублей будет составлять 1% от цены удочки (от 7200 рублей). Для этого мы полную цену 7200 рублей разделим на 100%: 7200/100 = 72 рубля (1% от полной цены удочки).
Теперь посчитаем, сколько в рублях будет составлять 40%-ная скидка. Для этого 72 руб (1%) умножим на 40 (размер скидки в процентах): 72 х 40 = 2880. Получается, что 40% скидки — это 2880 руб.
Нам остаётся от полной стоимости удочки (7200 рублей) отнять сумму скидки (2880 рублей): 7200 - 2880 = 4320. Это означает, что цена удочки с учётом скидки всего 4320 рублей. При расчёте в магазине нужно будет заплатить именно эту сумму.
Задача №2
Лида проходит курс по программированию, который состоит из 32 тем. (Как детям научиться программированию, читайте в статье). На данный момент она освоила 9 тем. Сколько процентов от программы курса прошла Лида?
Решение:Мы видим, что всего в курсе 32 темы, а пройденных Лидой 9. Примем общее количество тем курса за 100% (32 темы = 100%).
Выясним, сколько тем курса составляет 1%. Для этого нам необходимо общее число тем курса (32) разделить на 100 (100%): 32/100 = 0,32. Мы видим, что 1% курса — это это 32 сотые части темы. Не стоит пугаться, что количество тем получилось дробным. Лида ведь может пройти и не целую тему в какой-то момент времени.
Сейчас посчитаем, сколько Лида прошла тем в процентах, если в числах это 9. Нам нужно 7 разделить на 0,32 (1% от всего курса): 7/0,32 = 21,8. Лида прошла 21,8% курса программирования. Округляем полученное число в сторону большей величины и получаем ответ: 22%.
Задача №3
Мотоциклист едет из дома в гости к другу. Расстояние между их домами 52 километра. На данный момент он проехал 16 километров. Какой процент общего расстояния до дома друга проехал мотоциклист?
Решение:Проанализируем условия задачи. У нас есть общее расстояние, которое мотоциклисту нужно преодолеть: 52 километра. И расстояние, которое он уже проехал: 16 километров.
Условно примем всё расстояние 52 километра за 100%, для удобства расчётов, и вычислим, сколько километров составляет 1% от него. Для этого мы весь путь 52 километра разделим на 100 (%): 52/100 = 0,52 километра. Значит, 1% от всего расстояния 52 километра равен 0,52 километра (чуть более половины километра).
Находим, сколько процентов от 52 километров составляет 16 километров. Для этого разделим 16 километров на 0,52 (1% от всего расстояния): 16/0,52 = 30,7. Становится понятно, что 16 километров — это 30,7% от всего расстояния (52 километра). Округляем полученное число, и получаем 31%. Мотоциклист проехал 31% от всего пути в 52 км.
Игровые приёмы для объяснения процентов детям
Игровая и познавательная деятельность является ведущей для детей вплоть до позднего подросткового возраста. Поэтому объяснять проценты учащимся средней школы (время, когда они и проходят тему процентов в рамках школьной программы) будет особенно эффективно с применением игровых методик.
Первым и самым главным этапом для родителей и преподавателей, если они решили включить обучающий элемент в игру, будет выяснение интересов и предпочтений ребёнка (или детей, если речь идёт о школьном классе): кто-то охотно играет в «настолки» в команде, а кому-то более интересны активные игры на открытом воздухе с интерактивным подходом.
Продумайте, как ненавязчиво интегрировать тему процентов в игровой процесс:
Настольные игры.
Введите в настольную игру дополнительное правило: при вызове карты у игрока есть возможность получить бонус в виде процентов от заработанных ранее очков, если он их правильно подсчитает;
Сказки и рассказы с процентами.
Попробуйте придумывать вместе с ребёнком рассказы и истории, где персонажам необходимо решать задачи, связанные с процентами, чтобы преодолеть препятствия на пути к цели.
Можно также интегрировать их в уже известные сказки, где, например, Чародей даёт Принцессе задание на проценты, и, если она выполнит его верно, то сможет расколдовать своего возлюбленного Принца: «У меня было 700 граммов магического зелья. Я потратила 30% зелья, чтобы превратить принца в волка. Сколько зелья сейчас стоит в моём сундуке? Если ответишь правильно, так и быть, расколдую твоего ненаглядного».
Игры в магазин.
Историю с покупками и скидками можно переводить из реальности в игровой формат. Играйте с ребёнком один на один или собирайте его друзей и одноклассников, и стройте импровизированный магазин с разными товарами на карточках, где будут указаны цены. Выдайте детям определённую сумму игровых денег, и поставьте условие: кто сумеет купить на них большее количество товаров, тот получит приз. А для того, чтобы распорядиться деньгами наиболее рационально, нужно уметь рассчитывать сумму скидки на каждый товар, которая на ценниках указана в процентах.
Включение простых задачек на проценты в повседневные дела.
Покупая ребёнку конфеты или фрукты, ненавязчиво рассказывайте ему, что, если мы берём 20 персиков, это 100% покупки, значит 1% — это 2 персика. Дайте ученику подержать в руках 1% персиков: пусть он сопоставит разницу в количестве.
Спрашивайте, сколько процентов персиков останется, если он съест, скажем, 5 фруктов? Или поинтересуйтесь, сколько процентов апельсинов съела семья за неделю, если папа купил 10 штук, а осталось всего 2 апельсина.
Задания можно и нужно варьировать, чтобы поддерживать интерес и вовлеченность ребёнка в процесс.
Как объяснить проценты ребёнку, используя функции образовательной платформы iSmart?
Тема процентов далеко не самая простая для ученика средней школы, если только он не обладает выдающимися математическими способностями: на её освоение придётся потратить время, которого не всегда хватает в рамках школьных занятий. К тому же, не будем забывать, что в классе может учиться 15-20 учеников, и уделить всем должное внимание у преподавателя иногда нет физической возможности.
Чтобы не допустить отставания ребёнка от школьной программы, особенно, если проценты даются ему нелегко, необходимо подключать дополнительные занятия.
Сделать это профессионально, не прибегая к дорогостоящей помощи репетиторов, можно, зарегистрировавшись на образовательной платформе iSmart и занимаясь в удобное время и в любом месте (нужен только гаджет и доступ в Интернет).
iSmart — это интерактивный образовательный ресурс, в котором собрано более 300 тысяч заданий по всем предметам, включённым в школьную программу с 1 по 11 класс, а также раздел «Подготовка к школе» для дошкольников. Платформа сама подстраивается под запрос пользователя, если он следует простому алгоритму работы с ней:
Переходим во вкладку «Каталог заданий».
Выбираем предмет (нас в контексте темы процентов будет интересовать «Алгебра»), класс: «7-й», тему: «Числа и вычисления», подтему: «Три основные задачи на проценты, решение задач из реальной практики».
Получаем задание, и начинаем с ним работать.
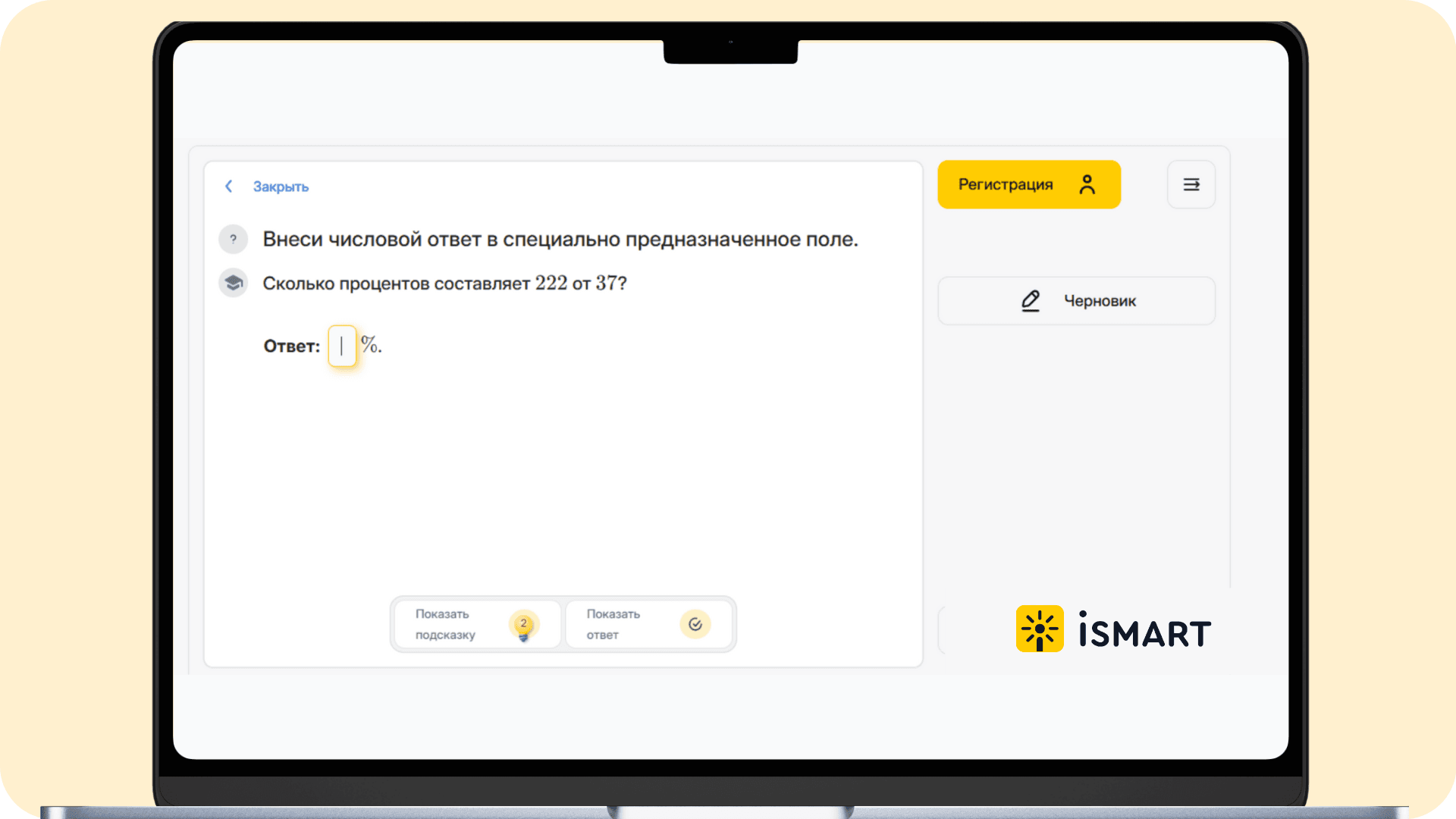
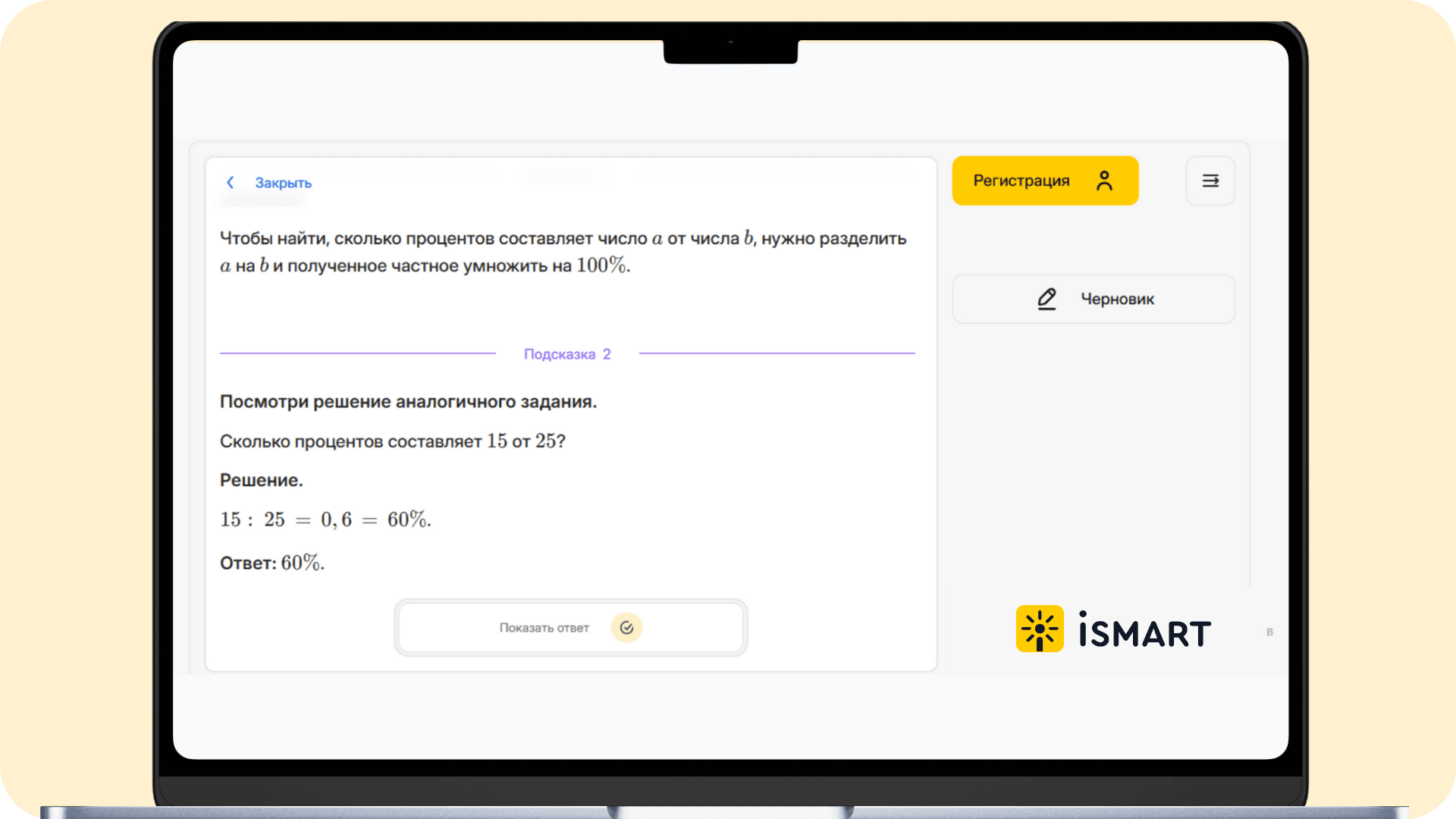
Следуя правилу и примеру из подсказки, делим 222 на 37, и получаем ответ: 600%.
Теперь проверим правильность решения, для чего нажимаем «Показать ответ», и «Подтвердить ответ» в поле в правом нижнем углу. Платформа поощрит вас ободряющей фразой, и предложит следующее задание для работы.
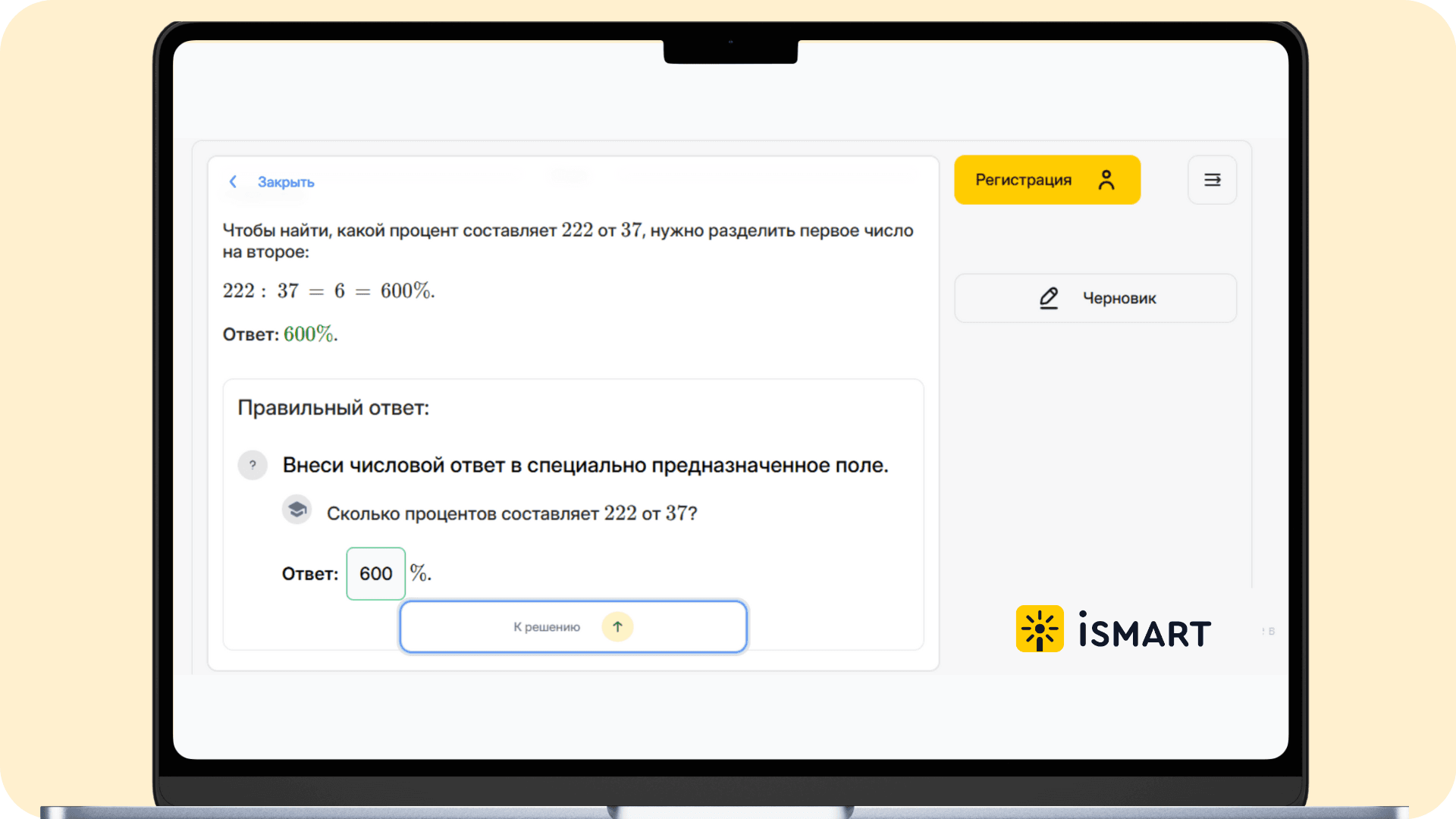
Платформа iSmart позволяет возвращаться к ранее пройденным темам. Например, если ребёнку не даётся понимание процентов, можно выбрать тему дробей, повторить, разобраться в ней детально, и лишь потом вернуться к задачам на проценты.
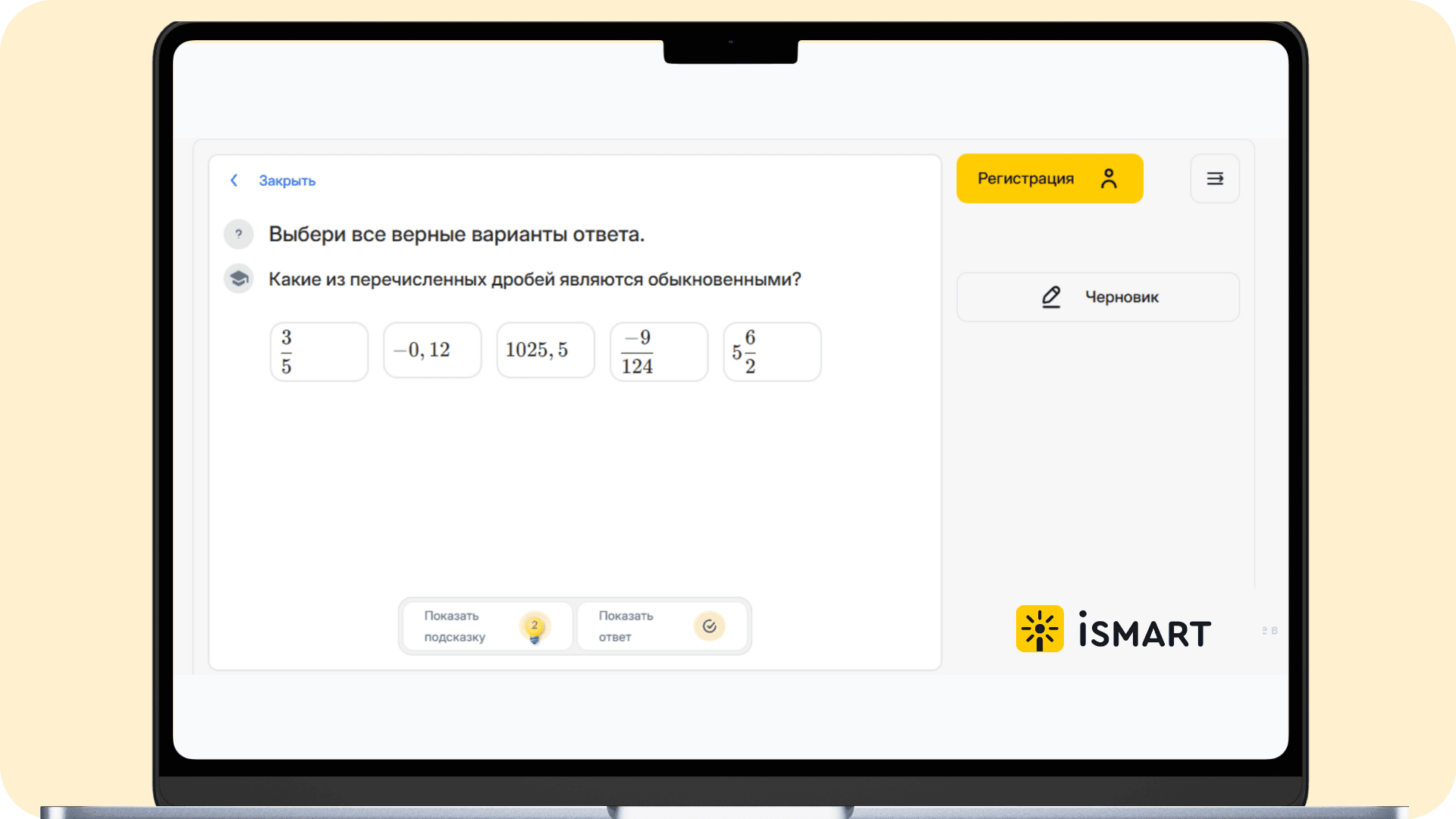
Платформа сконструирована таким образом, что у ребёнка нет возможности просто перескочить на следующее задание, не сделав предыдущее из лени или нежелания: условием доступа к новому заданию является верно решённая предшествующая задача.
Учащиеся средней школы уже могут работать с платформой самостоятельно, параллельно учась ориентироваться в цифровом пространстве.
В составлении заданий iSmart участвовали не только преподаватели профильных дисциплин, изучаемых в школе, но и детские психологи. Поэтому задания предлагаются ученикам с учётом их возрастных особенностей в ненавязчивой и увлекательной форме. Хватает 15-20 минут занятий в день, чтобы увидеть прогресс в успеваемости. На платформе дети не только учатся, но и (в зависимости от количества выполненных заданий) зарабатывают рейтинг и игровые смарткойны, которые можно использовать для игр на iSmart.
Комплексный подход к обучению и внимание к психологии ребёнка и его потребностям повышает мотивацию детей продолжать заниматься на платформе.
Чтобы обзавестись аккаунтом на iSmart (это необходимо для получения полного доступа ко всем функциям и закладкам платформы), пройдите простейшую регистрацию:
В левом верхнем углу нажмите «Мои дети», «Добавить ребёнка», и создайте детский аккаунт с весёлой аватаркой, где маленький пользователь сможет видеть задания, находящиеся у него в работе, рейтинг на платформе, и заработанные смарткойны.
Перейдите во вкладку «Каталог заданий», выберите предмет, класс, тему, и приступайте к работе.
Не откладывайте дополнительные занятия в долгий ящик! Регистрируйтесь на iSmart, и вы удивитесь, как быстро ваш ребёнок начнёт «щёлкать задачки на проценты, как орехи», и взлетит его успеваемость в школе по другим предметам!
Помните, ваши знания и достижения в ваших руках, а платформа iSmart сделает путь к успеху весёлым и комфортным!
Читать также





